Inspiriert von dieser Frage .

Bei einer Liste mit Zahlen drucken Sie:

• Die Summe und das Produkt der Zahlen in der Liste
• Der Durchschnitt und Median
• Die Unterschiede zwischen den einzelnen Begriffen in der Liste (ex [1,2,3] -> [1,1]: 1+1=2, 2+1=3)
• Die Liste, aufsteigend sortiert
• Das Minimum und Maximum der Liste
• Die Standardabweichung der Liste

Als Referenz:

Standardabweichung

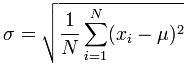
Wobei μ der mittlere Durchschnitt ist, ist x _i der idritte Term in der Liste und Ndie Länge der Liste.

Der kürzeste Code gewinnt. Viel Glück!

Q, 41

{(+/;*/;avg;med;-':;asc;min;max;dev)@\:x}

J, 73 70 Zeichen

((+/;*/;a;(<.@-:@#{/:~);2&-~/\;/:~;<./;>./;%:@:(a@:*:@:(-a)))[a=.+/%#)

Verwendungszweck:

   ((+/;*/;a;(<.@-:@#{/:~);2&-~/\;/:~;<./;>./;%:@:(a@:*:@:(-a)))[a=.+/%#)1 2 3 4
+--+--+---+-+-------+-------+-+-+-------+
|10|24|2.5|3|1 1 1 1|1 2 3 4|1|4|1.11803|
+--+--+---+-+-------+-------+-+-+-------+

TI-BASIC, 41 Bytes

1-Var Statsist ein Byte , und Σx, x̄usw. sind jeweils zwei Bytes.

Ans→L₁
1-Var Stats
SortA(L₁
Disp Σx,prod(Ans),x̄,Med,ΔList(Ans),L₁,minX,maxX,σx

Wenn das Ändern der Ausgabereihenfolge zulässig ist, kann ein Close-Paren gespeichert werden, wodurch die Punktzahl auf 40 Byte erhöht wird.

Q (87 Zeichen)

(sum;prd;avg;{.5*(sum/)x[((<)x)(neg(_)t;(_)neg t:.5*1-(#)x)]};(-':);asc;min;max;dev)@\:

z.B.

q) (sum;prd;avg;{.5*(sum/)x[((<)x)(neg(_)t;(_)neg t:.5*1-(#)x)]};(-':);asc;min;max;dev)@\: 10 9 8 7 6 5 4 3 2 1
55
3628800
5.5
5.5
10 -1 -1 -1 -1 -1 -1 -1 -1 -1
`s#1 2 3 4 5 6 7 8 9 10
1
10
2.872281

Ruby 187

O=->l{g=l.size
r=l.sort
s=l.inject(:+)+0.0
m=s/g
p s,l.inject(:*),m,g%2>0?r[g/2]:(r[g/2]+r[g/2-1])/2.0,l.each_cons(2).map{|l|l[1]-l[0]},r,r[0],r[-1],(l.inject(0){|e,i|e+(i-m)**2}/g)**0.5}

Verwendungssyntax: O[<array>] (zum Beispiel O[[1,2,3]])

Gibt alle erforderlichen Werte in der in der Frage angegebenen Reihenfolge an die Konsole aus.

IdeOne-Beispiele:

• mit ungerader Anzahl von Elementen: http://ideone.com/83ouj
• mit gerader Anzahl von Elementen: http://ideone.com/7PTRq

Scala 208 202 188:

val w=l.size
val a=l.sum/w
val s=l.sortWith(_<_)
Seq(l.sum,l.product,a,s((w+1)/2),(0 to w-2).map(i=>l(i+1)-l(i)),s,l.min,l.max,(math.sqrt((l.map(x=>(a-x)*(a-x))).sum*1.0/w))).map(println)

Prüfung:

scala> val l = util.Random.shuffle((1 to 6).map(p=>math.pow(2, p).toInt))
l: scala.collection.immutable.IndexedSeq[Int] = Vector(64, 8, 4, 32, 16, 2)

scala> val a=l.sum/l.size
a: Int = 21

scala> val s=l.sortWith(_<_)
s: scala.collection.immutable.IndexedSeq[Int] = Vector(2, 4, 8, 16, 32, 64)

scala> Seq(l.sum,l.product,a,s((s.size+1)/2),(0 to l.size-2).map(i=>l(i+1)-l(i)),l.sortWith(_<_),l.min,l.max,(math.sqrt((l.map(x=>(a-x)*(a-x))).sum*1.0/l.size))).map(println)
126
2097152
21
16
Vector(-56, -4, 28, -16, -14)
Vector(2, 4, 8, 16, 32, 64)
2
64
21.656407827707714

Julia 0,6 , 66 Bytes

x->map(f->f(x),[sum,prod,mean,median,diff,sort,extrema,std])|>show

Probieren Sie es online aus!

Julia 0,6 , 88 Bytes (unkorrigierter Standardentwickler, wie in op)

x->map(f->f(x),[sum,prod,mean,median,diff,sort,extrema,x->std(x,corrected=false)])|>show

Probieren Sie es online aus!

C ++ 14, 340 383 Bytes

Als generisches unbenanntes Lambda. Der erste Parameter List die Liste std::listvom Gleitkommatyp und der zweite Parameter ist der gewünschte Ausgabestream, wie z std::cout.

#import<cmath>
#define F(x);O<<x<<'\n';
#define Y l=k;++l!=L.end();
#define A auto
[](A L,A&O){A S=L;A l=L.begin(),k=l;A n=L.size();A s=*l,p=s,d=s*s,h=n/2.;for(S.sort(),Y s+=*l,p*=*l,d+=*l**l);for(l=S.begin();--h>0;++l)F(s)F(p)F(s/n)F(*l)for(Y)O<<*l-*k++<<","F(' ')for(A x:S)O<<x<<","F(' ')F(S.front())F(S.back())F(sqrt((d-s*s/n)/(n-1)))}

Kompiliert mit einer Warnung, C ++ erlaubt nicht "direkt gefolgt von Literalen wie F. Programm läuft noch.

• -1 & -2 Bytes dank Zacharý

Ungolfed:

#include<iostream>
#include<list>

#import<cmath>
#define F(x);O<<x<<'\n';
#define Y l=k;++l!=L.end();
#define A auto

auto f=
[](A L, A&O){
  A S=L;                  //copy the list for later sorting
  A l=L.begin(),          //main iterator
    k=l;                  //sidekick iterator
  A n=L.size();
  A s=*l,                 //sum, init with head of list
    p=s,                  //product, same
    d=s*s,                //standard deviation, formula see https://en.wikipedia.org/wiki/Algebraic_formula_for_the_variance
    h=n/2.;               //for the median later   
  for(
    S.sort(),             //now min/med/max is at known positions in S
    Y //l=k;++l!=L.end(); //skip the headitem-loop
    s += *l,              //l points the next element which is fine
    p *= *l,              //since the head given at definiten
    d += *l * *l          //needs the sum of the squares
  );
  for(
    l=S.begin();          //std::list has no random access
    --h>0;                //that's why single increment loop
    ++l                   //until median is crossed
  )
  F(s)  //;O<<s<<'\n';    //sum
  F(p)                    //product
  F(s/n)                  //average
  F(*l)                   //median (in S)
  for(Y) //l=k;++l!=L.end(); //set l back to L
    O<<*l-*k++<<","       //calc difference on the fly
  F(' ')
  for(A x:S)              //output sorted list
    O<<x<<"," 
  F(' ')
  F(S.front())            //minimum
  F(S.back())             //maximum
  F(sqrt((d-s*s/n)/(n-1))) //standard deviation
}

;


using namespace std;

int main() {
 list<double> l = {10,3,1,2,4};
 f(l, cout);
}

Perl 5 , 204 + 1 = 205 Bytes

@L=sort{$a<=>$b}@F;$p=1;$s+=$_,$p*=$_,$a+=$_/@F for@L;for(0..$#F){$o=($F[$_]-$a)**2/@F;push@d,$F[$_]-$F[$_-1]if$_}$o=sqrt$o;$m=@F%2?$F[@F/2]:$F[@F/2]/2+$F[@F/2-1]/2;say"$s $p$/$a $m$/@d$/@L$/@L[0,-1]$/$o"

Probieren Sie es online aus!

Pyt , 39 Bytes

←ĐĐĐĐĐĐĐŞ⇹Ʃ3ȘΠ4Șµ5Ș₋⇹6Ș↕⇹7ȘṀ↔Đе-²Ʃ⇹Ł/√

Dies gibt in der Reihenfolge den Median, das Produkt, die Differenzen, die umgekehrte Liste, die Summe, das Maximum und das Minimum, den Mittelwert und die Standardabweichung aus

Probieren Sie es online aus!

Erläuterung:

←ĐĐĐĐĐĐĐ                                              Push the array onto the stack 8 times
        ş                                             Sort in ascending order
         ⇹                                            Stack management
          Ʃ                                           Sum
           3Ș                                         Stack management
             Π                                        Product
              4Ș                                      Stack management
                µ                                     Mean (as a float)
                 5Ș                                   Stack management
                   ₋                                  Differences
                    ⇹6Ș                               Stack management
                       ↕                              Minimum and maximum
                        ⇹7Ș                           Stack management
                           Ṁ                          Median
                            ↔                         Stack management
                             Đе-²Ʃ⇹Ł/√               Standard Deviation

APL NARS, 119 Zeichen, 182 Bytes

{m←(s←+/w)÷n←⍴w←,⍵⋄s,(×/w),m,(n{j←⌊⍺÷2⋄2|⍺:⍵[1+j]⋄2÷⍨⍵[j]+⍵[j+1]}t),(⊂¯1↓(1⌽w)-w),(⊂t←w[⍋w]),(⌊/w),(⌈/w),√n÷⍨+/(w-m)*2}

Prüfung

  h←{m←(s←+/w)÷n←⍴w←,⍵⋄s,(×/w),m,(n{j←⌊⍺÷2⋄2|⍺:⍵[1+j]⋄2÷⍨⍵[j]+⍵[j+1]}t),(⊂¯1↓(1⌽w)-w),(⊂t←w[⍋w]),(⌊/w),(⌈/w),√n÷⍨+/(w-m)*2}
  ⎕fmt h 0 
┌9──────────────────────┐
│        ┌0─┐ ┌1─┐      │
│0 0 0 0 │ 0│ │ 0│ 0 0 0│
│~ ~ ~ ~ └~─┘ └~─┘ ~ ~ ~2
└∊──────────────────────┘
  ⎕fmt h 3
┌9──────────────────────┐
│        ┌0─┐ ┌1─┐      │
│3 3 3 3 │ 0│ │ 3│ 3 3 0│
│~ ~ ~ ~ └~─┘ └~─┘ ~ ~ ~2
└∊──────────────────────┘
  ⎕fmt h 1 2 3
┌9───────────────────────────────────────┐
│        ┌2───┐ ┌3─────┐                 │
│6 6 2 2 │ 1 1│ │ 1 2 3│ 1 3 0.8164965809│
│~ ~ ~ ~ └~───┘ └~─────┘ ~ ~ ~~~~~~~~~~~~2
└∊───────────────────────────────────────┘
  ⎕fmt h 1 2 3 4
┌9────────────────────────────────────────────────┐
│              ┌3─────┐ ┌4───────┐                │
│10 24 2.5 2.5 │ 1 1 1│ │ 1 2 3 4│ 1 4 1.118033989│
│~~ ~~ ~~~ ~~~ └~─────┘ └~───────┘ ~ ~ ~~~~~~~~~~~2
└∊────────────────────────────────────────────────┘
  ⎕fmt h 1 2 7 3 4 5 
┌9──────────────────────────────────────────────────────────────────┐
│                       ┌5──────────┐ ┌6───────────┐                │
│22 840 3.666666667 3.5 │ 1 5 ¯4 1 1│ │ 1 2 3 4 5 7│ 1 7 1.972026594│
│~~ ~~~ ~~~~~~~~~~~ ~~~ └~──────────┘ └~───────────┘ ~ ~ ~~~~~~~~~~~2
└∊──────────────────────────────────────────────────────────────────┘

Ocaml - 288 Bytes

Angenommen, die angegebene Liste ist eine nicht leere Liste von Floats (um Conversions zu vermeiden) und der zurückgegebene Median ist die schwache Definition des Medians:

median l = nso dass die Hälfte der Elemente von lkleiner oder gleich nund die Hälfte der Elemente von lgrößer oder gleich sindn

open List
let f=fold_left
let z=length
let s l=f(+.)0. l
let a l=(s l)/.(float_of_int(z l))let rec i=function|a::[]->[]|a::b->(hd b -. a)::(i b)let r l=let t=sort compare l in(s,f( *.)1. l,a t,nth t((z t)/2+(z t)mod 2-1),t,i l,nth t 0,nth t((z t)-1),sqrt(a(map(fun n->(n-.(a l))**2.)l)))

Die lesbare Version ist

open List

let sum l = fold_left (+.) 0. l
let prod l = fold_left ( *. ) 1. l
let avg l = (sum l) /. (float_of_int (length l))
let med l =
        let center = (length l) / 2 + (length l) mod 2 -1 in
        nth l center
let max l = nth l 0
let min l = nth l ((length l) - 1)
let dev l =
let mean = avg l in
        sqrt (avg (map (fun n -> (n -. mean)**2.) l))

let rec dif =
        function
        | a::[] -> []
        | a::b -> ((hd b) - a) :: (dif b)

let result l =
        let sorted = sort compare l in
        (
                sum sorted,
                prod sorted,
                avg sorted,
                med sorted,
                sorted,
                dif l,
                max sorted,
                min sorted,
                dev sorted
        )

PHP, 213 Bytes

function($a){echo$s=array_sum($a),_,array_product($a),_,$v=$s/$c=count($a);foreach($a as$i=>$x){$d+=($x-$v)**2;$i&&$f[]=$x-$a[$i-1];}sort($a);var_dump(($a[$c/2]+$a[$c/2+~$c%2])/2,$f,$a,$a[0],max($a),sqrt($d/$c));}

Probieren Sie es online aus .