Wie würde ich vorgehen, um eine Liste aller möglichen Permutationen einer Zeichenfolge mit einer Länge zwischen x und y zu erstellen, die eine variable Liste von Zeichen enthält?
Jede Sprache würde funktionieren, sollte aber portabel sein.
string
language-agnostic
cross-platform
UnkwnTech
quelle
quelle

Antworten:
Es gibt verschiedene Möglichkeiten, dies zu tun. Gängige Methoden verwenden Rekursion, Memoisierung oder dynamische Programmierung. Die Grundidee besteht darin, dass Sie eine Liste aller Zeichenfolgen der Länge 1 erstellen und dann in jeder Iteration für alle in der letzten Iteration erstellten Zeichenfolgen die mit jedem Zeichen in der Zeichenfolge verkettete Zeichenfolge einzeln hinzufügen. (Der Variablenindex im folgenden Code verfolgt den Beginn der letzten und der nächsten Iteration.)
Ein Pseudocode:
Sie müssten dann alle Zeichenfolgen mit einer Länge von weniger als x entfernen. Dies sind die ersten (x-1) * len (originalString) -Einträge in der Liste.
quelle
Es ist besser, Backtracking zu verwenden
quelle
Du wirst eine Menge Saiten bekommen, das ist sicher ...
Wobei Sie sie mit x und y definieren und r die Anzahl der Zeichen ist, aus denen wir auswählen - wenn ich Sie richtig verstehe. Sie sollten diese auf jeden Fall nach Bedarf generieren und nicht schlampig werden und beispielsweise ein Powerset generieren und dann die Länge der Zeichenfolgen filtern.
Das Folgende ist definitiv nicht der beste Weg, um diese zu generieren, aber es ist trotzdem interessant.
Knuth (Band 4, Faszikel 2, 7.2.1.3) sagt uns, dass die (s, t) -Kombination äquivalent zu s + 1 Dingen ist, die t zu einem Zeitpunkt mit Wiederholung genommen werden - eine (s, t) -Kombination ist eine Notation, die von verwendet wird Knuth das ist gleich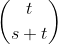 . Wir können dies herausfinden, indem wir zuerst jede (s, t) -Kombination in binärer Form (also der Länge (s + t)) erzeugen und die Anzahl der Nullen links von jeder 1 zählen.
. Wir können dies herausfinden, indem wir zuerst jede (s, t) -Kombination in binärer Form (also der Länge (s + t)) erzeugen und die Anzahl der Nullen links von jeder 1 zählen.
10001000011101 -> wird zur Permutation: {0, 3, 4, 4, 4, 1}
quelle
Nicht rekursive Lösung nach Knuth, Python-Beispiel:
quelle
"54321"nur EINEM String versuchen, wird (selbst) angezeigt .nextPermutation()es zustandslos ist - es werden nur die Eingaben zum Permutieren benötigt und Indizes werden nicht von Iteration zu Iteration verwaltet. Dies ist möglich, indem angenommen wird, dass die anfängliche Eingabe sortiert wurde, und Indizes (k0undl0) selbst gefunden werden, basierend darauf, wo die Reihenfolge beibehalten wird. Durch Sortieren einer Eingabe wie "54321" -> "12345" kann dieser Algorithmus alle erwarteten Permutationen finden. Da es jedoch eine Menge zusätzlicher Arbeit kostet, diese Indizes für jede generierte Permutation neu zu finden, gibt es effizientere Möglichkeiten, dies nicht rekursiv zu tun.Sie können sich " Effizientes Aufzählen der Teilmengen einer Menge " ansehen , in dem ein Algorithmus beschrieben wird, mit dem Sie einen Teil Ihrer Wünsche erfüllen können - generieren Sie schnell alle Teilmengen von N Zeichen von der Länge x bis y. Es enthält eine Implementierung in C.
Für jede Teilmenge müssten Sie noch alle Permutationen generieren. Wenn Sie beispielsweise 3 Zeichen von "abcde" möchten, gibt Ihnen dieser Algorithmus "abc", "abd", "abe" ... aber Sie müssten jedes einzelne permutieren, um "acb", "bac", zu erhalten. "bca" usw.
quelle
Einige funktionierende Java-Codes basierend auf Sarps Antwort :
quelle
Hier ist eine einfache Lösung in C #.
Es werden nur die unterschiedlichen Permutationen einer bestimmten Zeichenfolge generiert.
quelle
Hier gibt es viele gute Antworten. Ich schlage auch eine sehr einfache rekursive Lösung in C ++ vor.
Hinweis : Zeichenfolgen mit wiederholten Zeichen erzeugen keine eindeutigen Permutationen.
quelle
Ich habe das gerade in Ruby schnell ausgepeitscht:
Möglicherweise suchen Sie in der Sprach-API nach integrierten Funktionen für Permutationstypen, und Sie können möglicherweise optimierten Code schreiben. Wenn die Zahlen jedoch so hoch sind, bin ich mir nicht sicher, ob es viele Möglichkeiten gibt, viele Ergebnisse zu erzielen .
Wie auch immer, die Idee hinter dem Code ist, mit einer Zeichenfolge der Länge 0 zu beginnen und dann alle Zeichenfolgen der Länge Z zu verfolgen, wobei Z die aktuelle Größe in der Iteration ist. Gehen Sie dann jede Zeichenfolge durch und hängen Sie jedes Zeichen an jede Zeichenfolge an. Entfernen Sie am Ende alle, die unter dem x-Schwellenwert lagen, und geben Sie das Ergebnis zurück.
Ich habe es nicht mit potenziell bedeutungslosen Eingaben getestet (Nullzeichenliste, seltsame Werte von x und y usw.).
quelle
Dies ist eine Übersetzung von Mikes Ruby-Version in Common Lisp:
Und eine andere Version, die etwas kürzer ist und mehr Loop-Funktionen bietet:
quelle
Hier ist ein einfaches Wort C # rekursive Lösung:
Methode:
Berufung:
quelle
... und hier ist die C-Version:
quelle
Druckt alle Permutationen ohne Duplikate
quelle
Rekursive Lösung in C ++
quelle
Wenn Sie sich in Perl auf das Kleinbuchstabenalphabet beschränken möchten, können Sie Folgendes tun:
Dies gibt alle möglichen Zeichenfolgen zwischen 1 und 4 Zeichen mit Kleinbuchstaben. Für Großbuchstaben wechseln Sie
"a"zu"A"und"zzzz"zu"ZZZZ".Für gemischte Fälle wird es viel schwieriger und wahrscheinlich mit einem solchen eingebauten Perl-Operator nicht machbar.
quelle
Ruby Antwort, die funktioniert:
quelle
quelle
Die folgende Java-Rekursion druckt alle Permutationen einer bestimmten Zeichenfolge:
Es folgt die aktualisierte Version der obigen "permut" -Methode, mit der n! (n faktorielle) weniger rekursive Aufrufe im Vergleich zur obigen Methode
quelle
Ich bin mir nicht sicher, warum Sie das überhaupt tun möchten. Die resultierende Menge für mäßig große Werte von x und y ist riesig und wächst exponentiell, wenn x und / oder y größer werden.
Nehmen wir an, Ihr Satz möglicher Zeichen besteht aus 26 Kleinbuchstaben des Alphabets, und Sie fordern Ihre Anwendung auf, alle Permutationen mit der Länge = 5 zu generieren. Vorausgesetzt, Ihnen geht nicht der Speicher aus, erhalten Sie 11.881.376 (dh 26 hoch) von 5) Saiten zurück. Wenn Sie diese Länge auf 6 erhöhen, erhalten Sie 308.915.776 Saiten zurück. Diese Zahlen werden sehr schnell schmerzhaft groß.
Hier ist eine Lösung, die ich in Java zusammengestellt habe. Sie müssen zwei Laufzeitargumente angeben (entsprechend x und y). Habe Spaß.
quelle
Hier ist eine nicht rekursive Version, die ich mir in Javascript ausgedacht habe. Es basiert nicht auf Knuths oben nicht rekursivem, obwohl es einige Ähnlichkeiten beim Elementaustausch aufweist. Ich habe die Richtigkeit für Eingabearrays mit bis zu 8 Elementen überprüft.
Eine schnelle Optimierung wäre das Vorfliegen des
outArrays und das Vermeidenpush().Die Grundidee ist:
Generieren Sie bei einem einzelnen Quellarray einen ersten neuen Satz von Arrays, die das erste Element nacheinander mit jedem nachfolgenden Element austauschen, wobei die anderen Elemente jedes Mal ungestört bleiben. Beispiel: 1234 angegeben, 1234, 2134, 3214, 4231 erzeugen.
Verwenden Sie jedes Array aus dem vorherigen Durchgang als Startwert für einen neuen Durchgang. Tauschen Sie jedoch anstelle des ersten Elements das zweite Element mit jedem nachfolgenden Element aus. Nehmen Sie diesmal auch nicht das ursprüngliche Array in die Ausgabe auf.
Wiederholen Sie Schritt 2, bis Sie fertig sind.
Hier ist das Codebeispiel:
quelle
In Rubin:
Es ist ziemlich schnell, aber es wird einige Zeit dauern =). Natürlich können Sie bei "aaaaaaaa" beginnen, wenn die kurzen Saiten für Sie nicht interessant sind.
Ich hätte die eigentliche Frage vielleicht falsch interpretiert - in einem der Beiträge klang es so, als ob Sie nur eine Bruteforce-Bibliothek von Zeichenfolgen benötigen, aber in der Hauptfrage klingt es so, als müssten Sie eine bestimmte Zeichenfolge permutieren.
Ihr Problem ähnelt dem folgenden: http://beust.com/weblog/archives/000491.html (Listen Sie alle Ganzzahlen auf, in denen sich keine der Ziffern wiederholt, was dazu führte, dass viele Sprachen es mit dem Problem lösten Ocaml-Typ, der Permutationen verwendet, und ein Java-Typ, der noch eine andere Lösung verwendet).
quelle
Ich brauchte das heute und obwohl die bereits gegebenen Antworten mich in die richtige Richtung wiesen, waren sie nicht ganz das, was ich wollte.
Hier ist eine Implementierung mit der Heap-Methode. Die Länge des Arrays muss mindestens 3 betragen und darf aus praktischen Gründen nicht größer als 10 sein, je nachdem, was Sie tun möchten, Geduld und Taktrate.
Bevor Sie Ihre Schleife betreten, initialisieren Sie
Perm(1 To N)mit der ersten Permutation,Stack(3 To N)mit Nullen * undLevelmit2**. Am Ende des SchleifenaufrufsNextPerm, der false zurückgibt, wenn wir fertig sind.* VB erledigt das für Sie.
** Sie können NextPerm ein wenig ändern, um dies unnötig zu machen, aber es ist klarer.
Andere Methoden werden von verschiedenen Autoren beschrieben. Knuth beschreibt zwei, eine gibt die lexikalische Ordnung an, ist aber komplex und langsam, die andere ist als Methode der einfachen Änderungen bekannt. Jie Gao und Dianjun Wang haben ebenfalls eine interessante Arbeit geschrieben.
quelle
Wenn dieser Code in Python mit
allowed_charactersset to[0,1]und maximal 4 Zeichen aufgerufen wird, werden 2 ^ 4 Ergebnisse generiert:['0000', '0001', '0010', '0011', '0100', '0101', '0110', '0111', '1000', '1001', '1010', '1011', '1100', '1101', '1110', '1111']Hoffe, das nützt dir. Funktioniert mit jedem Zeichen, nicht nur mit Zahlen
quelle
Hier ist ein Link, der beschreibt, wie Permutationen einer Zeichenfolge gedruckt werden. http://nipun-linuxtips.blogspot.in/2012/11/print-all-permutations-of-characters-in.html
quelle
Obwohl dies Ihre Frage nicht genau beantwortet, gibt es eine Möglichkeit, jede Permutation der Buchstaben aus einer Reihe von Zeichenfolgen gleicher Länge zu generieren: Wenn Ihre Wörter beispielsweise "Kaffee", "Joomla" und "Moodle" waren, können Sie dies tun Erwarten Sie Ausgaben wie "coodle", "joodee", "joffle" usw.
Grundsätzlich ist die Anzahl der Kombinationen die (Anzahl der Wörter) hoch (Anzahl der Buchstaben pro Wort). Wählen Sie also eine Zufallszahl zwischen 0 und der Anzahl der Kombinationen - 1, konvertieren Sie diese Zahl in Basis (Anzahl der Wörter) und verwenden Sie dann jede Ziffer dieser Zahl als Indikator für das Wort, aus dem der nächste Buchstabe entnommen werden soll.
zB: im obigen Beispiel. 3 Wörter, 6 Buchstaben = 729 Kombinationen. Wählen Sie eine Zufallszahl: 465. Konvertieren Sie in Basis 3: 122020. Nehmen Sie den ersten Buchstaben von Wort 1, den zweiten von Wort 2, den dritten von Wort 2, den vierten von Wort 0 ... und Sie erhalten ... "Joofle".
Wenn Sie alle Permutationen möchten , führen Sie einfach eine Schleife von 0 bis 728 durch. Wenn Sie nur einen zufälligen Wert auswählen, ist es natürlich viel
einfacher,die Buchstaben zu durchlaufen, wenn Sie eine weniger verwirrende Methode verwenden. Mit dieser Methode können Sie eine Rekursion vermeiden, wenn Sie alle Permutationen wünschen. Außerdem sehen Sie so aus, als ob Sie Maths (tm) kennen !Wenn die Anzahl der Kombinationen zu groß ist, können Sie sie in eine Reihe kleinerer Wörter aufteilen und am Ende verketten.
quelle
c # iterativ:
quelle
quelle
Hier ist meine Einstellung zu einer nicht rekursiven Version
quelle
Die pythonische Lösung:
quelle
Nun, hier ist eine elegante, nicht rekursive O (n!) Lösung:
quelle