Ich glaube, ich werde begraben, weil ich so eine triviale Frage gestellt habe, aber ich bin etwas verwirrt über etwas.
Ich habe Quicksort in Java und C implementiert und einige grundlegende Vergleiche durchgeführt. Der Graph wurde als zwei gerade Linien dargestellt, wobei das C über 100.000 zufällige Ganzzahlen 4 ms schneller war als das Java-Gegenstück.
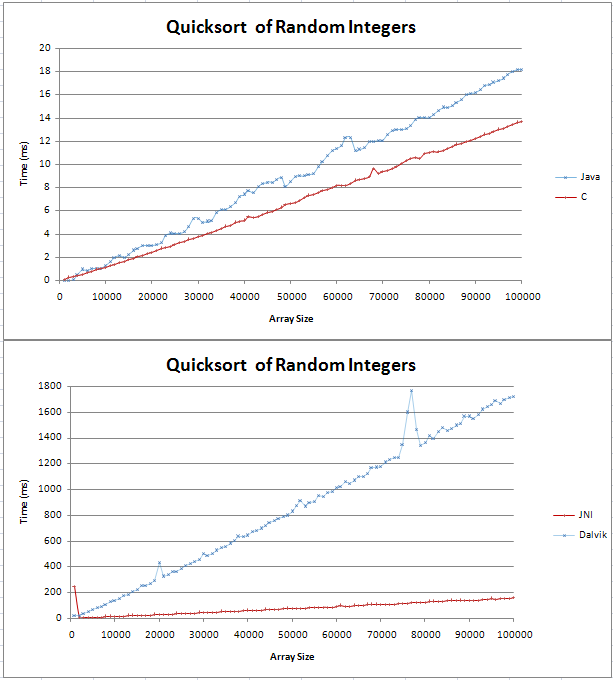
Den Code für meine Tests finden Sie hier;
Ich war mir nicht sicher, wie eine (n log n) Linie aussehen würde, aber ich dachte nicht, dass sie gerade sein würde. Ich wollte nur überprüfen, ob dies das erwartete Ergebnis ist und ob ich nicht versuchen sollte, einen Fehler in meinem Code zu finden.
Ich habe die Formel in Excel eingefügt und für Basis 10 scheint es eine gerade Linie mit einem Knick am Anfang zu sein. Liegt das daran, dass der Unterschied zwischen log (n) und log (n + 1) linear zunimmt?
Vielen Dank,
Gav

Antworten:
Wenn Sie das Diagramm vergrößern, sehen Sie, dass O (n logn) keine gerade Linie ist. Aber ja, es kommt dem linearen Verhalten ziemlich nahe. Um zu sehen warum, nehmen Sie einfach den Logarithmus einiger sehr großer Zahlen.
Zum Beispiel (Basis 10):
Um 1.000.000 Zahlen zu sortieren, fügt eine O (n logn) -Sortierung einen dürftigen Faktor 6 hinzu (oder nur ein bisschen mehr, da die meisten Sortieralgorithmen von Logarithmen der Basis 2 abhängen). Nicht sehr viel.
Tatsächlich ist dieser Log-Faktor so außerordentlich klein, dass etablierte O (n logn) -Algorithmen für die meisten Größenordnungen lineare Zeitalgorithmen übertreffen. Ein prominentes Beispiel ist die Erstellung einer Suffix-Array-Datenstruktur.
Ein einfacher Fall hat mich kürzlich gebissen, als ich versuchte, eine schnelle Sortierung von kurzen Saiten durch Verwendung der Radix-Sortierung zu verbessern . Es stellte sich heraus, dass diese (lineare Zeit-) Radix-Sortierung für kurze Zeichenfolgen schneller war als die Quicksortierung, aber es gab einen Wendepunkt für noch relativ kurze Zeichenfolgen, da die Radix-Sortierung entscheidend von der Länge der von Ihnen sortierten Zeichenfolgen abhängt.
quelle
Zu Ihrer Information, Quicksort ist eigentlich O (n ^ 2), aber mit einem durchschnittlichen Fall von O (nlogn)
Zu Ihrer Information, es gibt einen ziemlich großen Unterschied zwischen O (n) und O (nlogn). Deshalb ist es für keine Konstante an O (n) gebunden.
Eine grafische Demonstration finden Sie unter:
quelle
Um noch mehr Spaß in ähnlicher Weise zu haben, versuchen Sie, die von n Operationen benötigte Zeit in der Standarddatenstruktur für disjunkte Mengen zu zeichnen . Es wurde gezeigt, dass es asymptotisch n α ( n ) ist, wobei α ( n ) die Umkehrung der Ackermann-Funktion ist (obwohl Ihr übliches Lehrbuch für Algorithmen wahrscheinlich nur eine Grenze von n log log n oder möglicherweise n log * n zeigt ). Für jede Art von Zahl, auf die Sie wahrscheinlich als Eingabegröße stoßen, gilt α ( n ) ≤ 5 (und tatsächlich log * n ≤ 5), obwohl sie sich asymptotisch der Unendlichkeit nähert.
Ich nehme an, Sie können daraus lernen, dass asymptotische Komplexität zwar ein sehr nützliches Werkzeug zum Nachdenken über Algorithmen ist, aber nicht ganz dasselbe ist wie praktische Effizienz.
quelle
Daher ist O (n * log (n)) nur für eine kleine Datenmenge linear ähnlich.
Tipp: Vergessen Sie nicht, dass sich Quicksort bei zufälligen Daten sehr gut verhält und dass es sich nicht um einen O (n * log (n)) - Algorithmus handelt.
quelle
Alle Daten können auf einer Linie dargestellt werden, wenn die Achsen richtig gewählt sind :-)
Laut Wikipedia ist Big-O der schlechteste Fall (dh f (x) ist O (N) bedeutet, dass f (x) durch N "oben" begrenzt ist) https://en.wikipedia.org/wiki/Big_O_notation
Hier ist eine schöne Reihe von Grafiken, die die Unterschiede zwischen verschiedenen allgemeinen Funktionen darstellen: http://science.slc.edu/~jmarshall/courses/2002/spring/cs50/BigO/
Die Ableitung von log (x) ist 1 / x. So schnell steigt log (x) mit zunehmendem x. Es ist nicht linear, obwohl es wie eine gerade Linie aussehen kann, weil es sich so langsam biegt. Wenn ich an O (log (n)) denke, stelle ich es mir als O (N ^ 0 +) vor, dh die kleinste Potenz von N, die keine Konstante ist, da jede positive konstante Potenz von N sie schließlich überholen wird. Es ist nicht 100% genau, also werden Professoren sauer auf Sie, wenn Sie es so erklären.
Der Unterschied zwischen Protokollen zweier verschiedener Basen ist ein konstanter Multiplikator. Schlagen Sie die Formel zum Konvertieren von Protokollen zwischen zwei Basen nach: (hier unter "Basiswechsel": https://en.wikipedia.org/wiki/Logarithm ) Der Trick besteht darin, k und b als Konstanten zu behandeln.
In der Praxis treten bei den von Ihnen geplotteten Daten normalerweise Probleme auf. Es wird Unterschiede in Dingen außerhalb Ihres Programms geben (etwas, das vor Ihrem Programm in die CPU wechselt, Cache-Fehler usw.). Es dauert viele Läufe, um zuverlässige Daten zu erhalten. Konstanten sind der größte Feind beim Versuch, die Big O-Notation auf die tatsächliche Laufzeit anzuwenden. Ein O (N) -Algorithmus mit einer hohen Konstante kann langsamer sein als ein O (N ^ 2) -Algorithmus für ausreichend kleine N.
quelle
log (N) ist (sehr) ungefähr die Anzahl der Ziffern in N. Daher gibt es zum größten Teil kaum einen Unterschied zwischen log (n) und log (n + 1).
quelle
Versuchen Sie, eine tatsächliche lineare Linie darüber zu zeichnen, und Sie werden den kleinen Anstieg sehen. Beachten Sie, dass der Y-Wert bei 50.0000 kleiner ist als der 1/2 Y-Wert bei 100.000.
Es ist da, aber es ist klein. Deshalb ist O (nlog (n)) so gut!
quelle