Ich habe gerade über einen sortvis.org-Blog-Beitrag über Cyclesort gelesen . Dies ist wahrscheinlich das dunkelste, von dem ich bisher gehört habe, da es Mathematik verwendet, mit der ich nicht vertraut bin (Erkennen von Zyklen in Permutationen von Ganzzahlensätzen).
Was ist das dunkelste, das du kennst?
algorithms
sorting
sova
quelle
quelle

Antworten:
Schon mal was von Geduldssortierung gehört ? Na jetzt hast du ...
quelle
Slowsort funktioniert durch Multiplizieren und Aufgeben (im Gegensatz zu Teilen und Erobern). Es ist interessant, weil es nachweislich der am wenigsten effiziente Sortieralgorithmus ist, der erstellt werden kann (asymptotisch und mit der Einschränkung, dass ein solcher Algorithmus, obwohl er langsam ist, die ganze Zeit auf ein Ergebnis hinarbeiten muss).
Dies gleicht es von Bogosort aus, da Bogosort im besten Fall sehr effizient ist - und zwar, wenn das Array bereits sortiert ist. Slowsort „leidet“ nicht unter einem solchen Best-Case-Verhalten. Es hat auch im besten Fall noch Laufzeit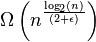 für ϵ > 0.
für ϵ > 0.
Hier ist der Pseudocode aus dem Wikipedia-Artikel :
quelle
Ich weiß nicht, ob dies als obskur gilt, aber einer der lächerlichsten "Sortieralgorithmen" ist Bogosort . Die Links von der Bogosort-Seite machen auch Spaß.
Und da ist dieses Juwel aus der Sektion "Quanten-Bogo-Sort".
Hmmm ... das könnte man so sagen :-).
quelle
Ein anderer obskurer "Algorithmus" ist Intelligent Design Sort - aber kein Algorithmus ist schneller oder hat einen geringeren Speicherverbrauch :)
quelle
Sleep Sort ist ziemlich neuartig.
quelle
Ich denke, die Blasenart wäre auch in dieser Situation die falsche Antwort
:)
quelle
Knuth Volume 3 1 enthält in der Antwort auf eine der Übungen eine Implementierung eines namenlosen Sortieralgorithmus, der im Grunde genommen ein uralter Codegolf ist - die kürzeste Sortierung, die Sie in der MIX-Assemblersprache schreiben können. Der Kurzcode ist allerdings für den ach so geringen Preis von O (N 3 ) -Komplexität erhältlich ...
1 Zumindest in den älteren Ausgaben. Angesichts der Änderungen an MIXAL für die neue Edition bin ich mir nicht sicher, ob es noch vorhanden ist oder ob es überhaupt Sinn macht, was im Original-MIXAL passiert ist.
quelle
Für meine Datenstrukturklasse musste ich (explizit) die Korrektheit der Stooge-Sortierung nachweisen . Es hat eine Laufzeit von O (n ^ {log 3 / log 1,5}) = O (n ^ 2,7095 ...).
quelle
Ich weiß nicht, ob es die dunkelste ist, aber Spaghetti-Sorte ist eine der besten in Situationen, in denen Sie sie verwenden können.
quelle
Eines der ursprünglichen Bücher von Knuth, "Sortieren und Suchen", hatte eine mittlere Ausklappung, die einen Vorgang zeigte, bei dem eine Banddatei ohne Festplatte sortiert wurde. Ich denke, es wurden sechs Bandlaufwerke verwendet, und es wurde explizit gezeigt, wann jedes vorwärts, rückwärts, rückwärts oder im Leerlauf gelesen wurde. Heute ist es ein Denkmal für eine veraltete Technologie.
quelle
Ich habe einmal eine Blasensortierung in Vektorregistern in CRAY Assembler durchgeführt. Die Maschine hatte einen Doppelschiebebefehl, mit dem Sie den Inhalt eines Vektorregisters um ein Wort nach oben / unten verschieben konnten. Tragen Sie jeden zweiten Punkt in zwei Vektorregister ein, dann können Sie eine vollständige Blasensortierung durchführen, ohne jemals eine weitere Speicherreferenz erstellen zu müssen, bis Sie fertig sind. Mit Ausnahme des N ** 2-Charakters der Blasensorte war es effizient.
Ich musste auch einmal eine Gleitkomma-Sortierung eines Vektors der Länge 4 für eine einzelne Sortierung so schnell wie möglich durchführen. Haben Sie es durch Tabellensuche gemacht (das Vorzeichenbit von A2-A1 ist ein Bit, das Vorzeichen von A3-A1 bildet ein anderes Bit ..., dann suchen Sie den Permutationsvektor in einer Tabelle nach. Es war tatsächlich die schnellste Lösung, die ich finden konnte Funktioniert auf modernen Architekturen jedoch nicht gut, da Floating- und Integer-Einheiten zu getrennt sind.
quelle
Google Code Jam hatte ein Problem mit einem Algorithmus namens Gorosort, den sie meiner Meinung nach für dieses Problem erfunden haben.
http://code.google.com/codejam/contest/dashboard?c=975485#s=p3
quelle
Ich erinnere mich nicht an den Namen, aber es war im Grunde genommen
quelle
Shell sortieren
Vielleicht ist der Algorithmus selbst nicht so dunkel, aber wer kann eine Implementierung nennen, die tatsächlich in der Praxis verwendet wird? Ich kann!
TIGCC (ein GCC-basierter Compiler für TI-89/92 / V200-Grafikrechner) verwendet die Shell-Sortierung für die
qsortImplementierung in seiner Standardbibliothek:Shell-Sortierung wurde zugunsten von QuickSort gewählt, um die Codegröße niedrig zu halten. Obwohl die asymptotische Komplexität schlechter ist, verfügt der TI-89 nicht über viel RAM (190 KB, abzüglich der Programmgröße und der Gesamtgröße aller nicht archivierten Variablen), sodass davon auszugehen ist, dass die Anzahl der Elemente größer ist niedrig sein.
Eine schnellere Implementierung wurde geschrieben, nachdem ich mich darüber beschwert hatte, dass es in einem Programm, das ich schrieb, zu langsam sei. Es werden bessere Spaltgrößen sowie Optimierungen der Baugruppe verwendet. Es kann hier gefunden werden: qsort.c
quelle