Diese Frage ergibt sich aus meiner tatsächlichen Verwirrung darüber, wie ich entscheiden soll, ob ein Logistikmodell gut genug ist. Ich habe Modelle, die den Zustand von Paaren zwei Jahre nach ihrer Bildung als abhängige Variable als Einzelprojekt verwenden. Das Ergebnis ist erfolgreich (1) oder nicht (0). Ich habe unabhängige Variablen zum Zeitpunkt der Bildung der Paare gemessen. Mein Ziel ist es zu testen, ob eine Variable, von der ich vermutete, dass sie den Erfolg der Paare beeinflusst, sich auf diesen Erfolg auswirkt und andere potenzielle Einflüsse kontrolliert. In den Modellen ist die interessierende Variable signifikant.
Die Modelle wurden mit der glm()Funktion in geschätzt R. Um die Qualität der Modelle zu beurteilen, habe ich einige Dinge getan: glm()gibt Ihnen die residual deviance, die AICund die BICStandardeinstellung. Außerdem habe ich die Fehlerrate des Modells berechnet und die gebündelten Residuen geplottet.
- Das komplette Modell hat eine kleinere Restabweichung, AIC und BIC als die anderen Modelle, die ich geschätzt habe (und die im kompletten Modell verschachtelt sind), was mich zu der Annahme veranlasst, dass dieses Modell "besser" ist als die anderen.
- Die Fehlerrate des Modells ist meiner Meinung nach relativ niedrig (wie bei Gelman und Hill, 2007, S. 99 ):
error.rate <- mean((predicted>0.5 & y==0) | (predicted<0.5 & y==1)bei etwa 20%.
So weit, ist es gut. Wenn ich jedoch die gebündelten Residuen zeichne (wiederum gemäß den Empfehlungen von Gelman und Hill), fällt ein großer Teil der Bins außerhalb des 95% -KI:
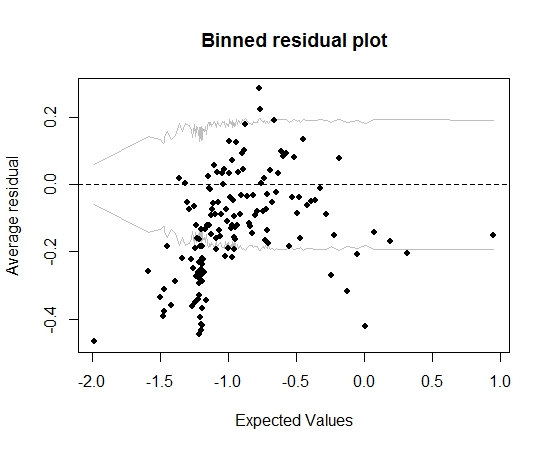
Diese Handlung lässt mich glauben, dass etwas an dem Modell völlig falsch ist. Sollte das mich dazu bringen, das Modell wegzuwerfen? Sollte ich anerkennen, dass das Modell nicht perfekt ist, es aber behalten und die Auswirkung der interessierenden Variablen interpretieren? Ich habe mit dem Ausschließen von Variablen und einigen Transformationen herumgespielt, ohne die Darstellung der gebündelten Residuen wirklich zu verbessern.
Bearbeiten:
- Derzeit verfügt das Modell über ein Dutzend Prädiktoren und 5 Interaktionseffekte.
- Die Paare sind "relativ" unabhängig voneinander in dem Sinne, dass sie alle in einer kurzen Zeitspanne (aber nicht genau genommen alle gleichzeitig) gebildet werden und es viele Projekte (13.000) und viele Einzelpersonen (19.000) gibt ), so dass ein nicht unerheblicher Teil der Projekte nur von einer Person bearbeitet wird (es gibt ungefähr 20000 Paare).
quelle

Antworten:
Die Klassifizierungsgenauigkeit (Fehlerrate) ist eine falsche Bewertungsregel (optimiert durch ein Scheinmodell), die willkürlich, diskontinuierlich und leicht zu manipulieren ist. Es wird in diesem Zusammenhang nicht benötigt.
Sie haben nicht angegeben, wie viele Prädiktoren es gab. Anstatt die Modellanpassung zu beurteilen, wäre ich versucht, das Modell einfach anzupassen. Ein Kompromissansatz besteht darin, anzunehmen, dass Interaktionen nicht wichtig sind, und kontinuierliche Prädiktoren mithilfe von Regressionssplines nichtlinear sein zu lassen. Zeichnen Sie die geschätzten Beziehungen. Das
rmsPaket in R macht das alles relativ einfach. Weitere Informationen finden Sie unter http://biostat.mc.vanderbilt.edu/rms .Sie können sich mit "Paaren" befassen und feststellen, ob Ihre Beobachtungen unabhängig sind.
quelle
quelle