Nach Ladners Theorem gibt es unendlich viele N P -Intermediat- ( N P I ) -Probleme , wenn ist . Es gibt auch natürliche Kandidaten für diesen Status, wie zum Beispiel Graph Isomorphism, und eine Reihe anderer, siehe Probleme zwischen P und NPC . Dennoch ist die überwiegende Mehrheit in der Menge der bekannten n ein t u r ein l N P ist bekannt -Probleme entweder in seine P oder N P C . Nur ein kleiner Teil von ihnen bleibt ein Kandidat für die N P I . Mit anderen Worten, wenn wir zufällig ein natürliches -Problem unter den bekannten auswählen, haben wir sehr wenig Chance, einen N P I -Kandidaten auszuwählen . Gibt es eine Erklärung für dieses Phänomen?
Ich könnte mir 3 mögliche Erklärungen ausdenken, mehr auf der philosophischen Seite:
Der Grund für einen so geringen Anteil an natürlichen -Kandidaten ist, dass sich N P I letztendlich als leer herausstellen wird. Ich weiß, das impliziert P = N P , also ist es sehr unwahrscheinlich. Dennoch könnte man noch streiten (obwohl ich nicht einer von ihnen bin) , dass die Seltenheit der natürlichen N P I Probleme ist eine empirische Beobachtung , dass erscheint tatsächlich zur Unterstützung P = N P , im Gegensatz zu den meisten anderen Beobachtungen.
Die Kleinheit von "natural- " stellt eine Art scharfen Phasenübergang zwischen einfachen und harten Problemen dar. Anscheinend verhalten sich die bedeutungsvollen, natürlichen algorithmischen Probleme so, dass sie entweder einfach oder schwierig sind. Der Übergang ist eng (aber immer noch vorhanden).
Das Argument in 2 kann auf die Spitze getrieben werden: schließlich alle Probleme in "natur- " wird in gesetzt werden P ∪ N P C , noch P ≠ N P , so N P I ≠ ∅ . Dies würde bedeuten, dass alle verbleibenden Probleme in N P I sindsind "unnatürlich" (erfunden, ohne realen Sinn). Eine Interpretation davon könnte sein, dass natürliche Probleme entweder leicht oder schwer sind; der Übergang ist nur ein logisches Konstrukt ohne "physikalische" Bedeutung. Dies erinnert ein wenig an irrationale Zahlen, die durchaus logisch sind, aber nicht als Messwert einer physikalischen Größe auftreten. Als solche kommen sie nicht aus der physischen Realität, sondern befinden sich im "logischen Verschluss" dieser Realität.
Welche Erklärung magst du am liebsten oder kannst du eine andere vorschlagen?
quelle




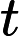
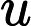





Antworten:
Wie andere darauf hingewiesen haben, ist es fraglich, inwieweit das, was Sie zu erklären versuchen, überhaupt wahr ist. Man könnte argumentieren, dass sich theoretische Informatiker in den 60er und 70er Jahren nur mehr für die Art von Problemen interessierten , die sich entweder als P- oder NP-vollständig herausstellen. Aufgrund des Aufstiegs der Komplexitätstheoretischen Kryptographie, des Quantencomputers, der Gitter usw. sowie der einfachen Tatsache, dass die NP-Vollständigkeit so gut verstanden wurde, hat unser Interesse zugenommen die Art von Problemen, die sich als NP-intermediär herausstellen.
Dennoch könnte man fragen: In dem Maße, in dem die Sache wahr ist - in dem Maße, in dem so viele natürliche Such- und Optimierungsprobleme entweder NP-vollständig oder aber in P - in diesem Ausmaß "einrasten" , warum ist es wahr? Hier, glaube ich, kann man eine Menge Intuition gewinnen, wenn man sich ein früheres Phänomen von der Berechenbarkeit ansieht: dass so viele natürliche Rechenmodelle "einrasten", um Turing-vollständig zu sein. In diesem Fall würde ich sagen, dass die Erklärung lautet, dass es schwer zu vermeiden ist, wenn Sie ein paar grundlegende Komponenten haben - einen Lese- / Schreibspeicher, Schleifen, Bedingungen usw. -in der Lage sein, eine Turing-Maschine zu simulieren und somit Turing-vollständig zu sein. Genauso ist es schwer zu vermeiden, dass ein Such- oder Optimierungsproblem einige grundlegende Komponenten aufweist - vor allem die Fähigkeit, "Gadgets" zu konstruieren, die logische Gatter wie AND, OR und NOT imitieren SAT zu codieren und damit NP-vollständig zu sein.
So wie ich es mir vorstelle, üben Probleme wie SAT eine starke "Anziehungskraft" auf alle anderen Rechenprobleme in ihrer Umgebung aus, was sie dazu veranlasst, auch NP-vollständig zu werden. Normalerweise bedarf es keiner besonderen Erklärung, wenn noch ein weiteres Problem diesem Zug erliegt! Bemerkenswerter und erklärungsbedürftiger ist es, wenn ein (anscheinend) hartes NP-Problem eine Eigenschaft aufweist, die es der Anziehungskraft von SAT widersteht . Dann wollen wir wissen: Was ist das für eine Eigenschaft? Warum können Sie für dieses Problem nicht den üblichen Trick der NP-Vollständigkeit spielen, nämlich Gadgets zu konstruieren, die boolesche Logikgatter codieren? Ich habe in der letzten CS.SE-Antwort eine Liste mit allgemeinen Antworten auf diese Frage zusammengestellt, aber (wie ein anderer Kommentator bereits betont hat) es gibt andere mögliche Antworten, die ich verpasst habe.
quelle
Viele natürliche Probleme können als Constraint Satisfaction Problems ausgedrückt werden, und es gibt Dichotomiesätze für CSPs.
quelle
Nur ein Scherz: Nachdem ich über die "SAT-Anziehungskraft" in der netten Antwort von Scott Aaronson nachgedacht hatte, kam mir eine andere Metapher in den Sinn: das 3-SAT-2-SAT-Sandwich !
... aber ich weiß nicht, ob das Sandwich mit natürlichen Zutaten gefüllt werden kann (ich fand jedoch, dass es mit etwas ( 2 + ( log n ) k gefüllt werden kann )-SAT-Sauce [1], wenn die Exponential-Zeit-Hypothese wahr ist) :-D
Ein weiteres Ergebnis in [1] ist, dass es nicht mit gefüllt werden kann , 0 < filled < 2 .







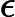




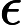


[1] Yunlei Zhao, Xiaotie Deng, CH Lee, Hong Zhu, -SAT und seine Eigenschaften







quelle
Wir können eine vierte Möglichkeit nicht ausschließen, dass es viele natürliche -zwischenprobleme gibt. Die offensichtliche Knappheit ist auf den Mangel an notwendigen Techniken und Werkzeugen zurückzuführen, die erforderlich sind, um den N P -Zwischenstatus unter einer plausiblen Komplexitätsvermutung nachzuweisen (Arora und Barak stellten fest, dass wir den N P -Zwischenstatus eines natürlichen N P- Problems nicht nachweisen können, selbst wenn P angenommen wird ≠ N P ).











Es scheint, dass die Schleusen der natürlichen -Zwischenprobleme offen sind. Jonsson, Lagerkvist und Nordh erweiterten die Diagonalisierungstechnik von Ladner, die als Lückenbildung bei Problemen bekannt ist , und wandten sie auf Constraint Satisfaction Problems an. Sie erhielten einen CSP, der ein Kandidat für den N P -Intermediate-Status ist. Sie bewiesen, dass das Problem der propositionellen Abduktion N P -Zwischenfragmente aufweist.





Auch Grohe die Existenz bewiesen -Zwischenerzeugnis CSP Probleme unter der Annahme , dass F P T ≠ W [ 1 ] . Er erhielt solche Probleme, indem er die Baumbreite der entsprechenden Urgraphen einschränkte.









Referenzen :
1- M. Grohe. Die Komplexität von Homomorphismus- und Bedingungszufriedenheitsproblemen von der anderen Seite gesehen. Journal of the ACM, 54 (1), Artikel 1, 2007
2. Peter Jonsson, Victor Lagerkvist und Gustav Nordh. Blasen von Löchern in verschiedenen Aspekten von Rechenproblemen mit Anwendungen zur Einschränkung der Zufriedenheit. In Proceedings der 19. Internationalen Konferenz über Prinzipien und Praktiken der Constraint-Programmierung (CP-2013). 2013.
quelle
Hier ist ein Märchen über die Goldlöckchen-Struktur von NP-Zwischenproblemen. (Warnung: Diese Geschichte mag ein nützlicher Irrtum sein, um potenzielle Hypothesen zu generieren und zu testen, aber sie ist nicht dazu gedacht, wissenschaftlich streng zu sein. Sie basiert auf einer Exponential-Zeit-Hypothese, einem Schuss Kolmogorov-Komplexitätsmagie, und einigen Stücken, die aus der SAT-Theorie entlehnt wurden Lösen und heuristische Trichotomie von Terence Tao für Probleme. Konsumieren auf eigenes Risiko, wie bei allen handwedelnden mathematischen Erfindungen.)
Wenn fast alle Instanzen in einem Problem in NP stark strukturiert sind, liegt das Problem tatsächlich in P. Die Instanzen enthalten somit fast alle viel Redundanz, und ein Polynom-Zeit-Algorithmus für das Problem ist ein Weg, die Redundanz herauszufiltern. Es ist sogar vorstellbar, dass jedes Problem in P erhalten werden kann, indem ein Problem in EXP genommen und eine strukturierte Redundanz hinzugefügt wird, und zwar über irgendeine Form von Auffüllung (nicht notwendigerweise die übliche Art). Wenn dies der Fall wäre, könnte ein Polynom-Zeit-Algorithmus als ein effizienter Weg angesehen werden, um diese Auffüllung rückgängig zu machen.
Wenn es genügend Instanzen gibt, die nicht strukturiert sind und einen "Kern der Härte" bilden, ist das Problem NP-vollständig.
Wenn dieser "Kern der Härte" jedoch zu dünn ist, hat er nur Platz, um etwas von SAT darzustellen, sodass das Problem bei P- oder NP-Intermediaten liegt. (Dieses Argument ist das Wesen von Ladners Satz). Um Scotts Analogie zu verwenden, übt der "Kern der Härte" eine Anziehungskraft auf das Problem aus, indem er NP-vollständig ist. Die Instanzen im "Kern der Härte" enthalten nicht viel Redundanz, und der einzige realistische Algorithmus, der für all diese Instanzen funktioniert, ist die Brute-Force-Suche (natürlich funktioniert auch die Tabellensuche, wenn es nur endlich viele gibt).
Unter diesem Gesichtspunkt sollten NP-intermediäre Probleme in der Praxis selten sein, da sie ein feines Goldlöckchen-Gleichgewicht zwischen Instanzen erfordern, die strukturiert und unstrukturiert sind. Instanzen sollten über genügend Redundanz verfügen, damit sie teilweise für einen Algorithmus zugänglich sind, aber es sollte genug von einem Härtekern vorhanden sein, auf den das Problem nicht zutrifft.
Man kann eine noch einfachere (und amüsantere, aber möglicherweise noch irreführendere) Geschichte erzählen, die auf Rätseln basiert. Mit nur wenigen Einschränkungen kann man eine Menge Suche erzwingen, zum Beispiel ist NxN Sudoku NP-vollständig. Nun überlegen Sie, ob Sie gebeten werden, viele kleine Rätsel auf einmal zu lösen (z. B. viele 9x9-Sudokus). Die benötigte Zeit wird in etwa linear in Bezug auf die Anzahl der Rätsel in jedem Fall sein, und dieses Problem ist dann in P. Bei Zwischenproblemen kann man sich vorstellen, dass jeder Fall eine große (aber nicht zu große) Anzahl von Sudokus im Großen ist (aber nicht zu große) Gitter. Der Grund, warum wir nicht viele solcher Probleme beobachten, ist, dass sie trostlos zu stellen und zu lösen wären!
quelle
quelle