Der Kalman-Filteralgorithmus funktioniert wie folgt
Initialisiere und .
Bei jeder Iteration ist
Vorhersagen
Vorausgesagte (a priori) Zustandsschätzung Vorhergesagte (a priori) geschätzte Kovarianz Aktualisieren
Innovations- oder Messrest Innovation (oder Rest) Kovarianz Optimaler Kalman-Gewinn Statusschätzung (a posteriori) aktualisiert Aktualisiert (a posteriori) Schätze die Kovarianz
Die Kalman-Verstärkung repräsentiert die relative Wichtigkeit des Fehlers in Bezug auf die vorherige Schätzung .
Ich frage mich, wie ich die Formel für den Kalman-Gewinn intuitiv verstehen kann . Betrachten Sie den Fall, wenn die Zustände und Ausgänge skalar sind, warum ist die Verstärkung größer, wenn
ist größer
ist größer
ist kleiner?
Danke und Grüße!
quelle















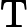

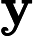
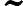
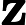



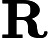
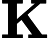

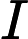

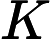
Antworten:
Ich fand eine gute Art, intuitiv an Kalman Gain denken . Wenn Sie schreiben auf diese Weise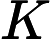
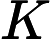
Sie werden feststellen, dass die relativen Größen der Matrizen ( ) und ( ) eine Beziehung zwischen der Verwendung der vorhergesagten Zustandsschätzung ( ) und der Messung ( ) durch den Filter .




 ⁻
⁻ỹ
Einsetzen der ersten Grenze in die Messungsaktualisierungsgleichung
Wenn die Größe von klein ist, was bedeutet, dass die Messungen genau sind, hängt die Zustandsschätzung hauptsächlich von den Messungen ab.
Wenn der Zustand genau bekannt ist, ist im Vergleich zu klein , und der Filter ignoriert meist die Messungen, die sich stattdessen auf die aus dem vorherigen Zustand abgeleitete Vorhersage ( ).
 ⁻
⁻



 ⁻
⁻
quelle
Die Kalman-Verstärkung gibt an, um wie viel ich meine Schätzung bei einer Messung ändern möchte.
Umgekehrt, wenn klein ist, dann wissen Sie, dass sich Ihr Zustand nicht so stark ändert, sodass Sie Ihre Schätzungen nicht zu sehr zu jedem Zeitpunkt ändern möchten. @ Jav_Rocks Antwort besagt, dass wenn , dann der . Mit anderen Worten, er implizierte, dass Sie nicht mehr versuchen, Ihre Schätzung zu ändern, wenn Sie glauben, dass sich Ihr Zustand nicht mehr ändert.





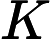


quelle
Jav_Rock hat es verstanden. Eigentlich , wenn Sie schreiben wie folgt aus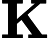
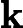
Der Zähler des Bruchs steht für die vom Modell ausgehende Unsicherheit, während für die Unsicherheit aus der Messung steht. Der Wert des Bruchs gibt also an, wie sehr wir der Messung vertrauen sollten, wie von Jav_Rock erklärt.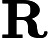
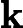
Was , wird die Beobachtung nur in den Zustand zurückverwandelt, da es sich um den Zustand handelt, den wir aktualisieren möchten, nicht um die Beobachtung.

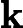
Zum Abschluss berechnet die Verstärkung wie viel Korrektur wir von der Beobachtung nehmen und die Korrektur der Beobachtung zurück in die Zustandskorrektur transformieren sollten, was zur Aktualisierung der Zustandsschätzung führt: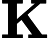
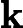
quelle
Ich arbeite am Kalman Filter (KF) -Algorithmus. Ich beobachtete, dass sich die Kalman-Verstärkung mit der Konvergenz des Algorithmus mit der Zeit befasst, das heißt, wie schnell der Algorithmus die Residuen korrigiert und minimiert.
Wenn Sie zur Gleichung kommen, wählen Sie einen anfänglichen Kalman-Verstärkungswert und variieren Sie ihn von niedrig nach hoch, so dass Sie einen angenäherten erhalten.
quelle