In ihrer Arbeit über Autoencoder für die Textklassifizierung demonstrierten Hinton und Salakhutdinov die Darstellung der zweidimensionalen LSA (die eng mit PCA verwandt ist) : 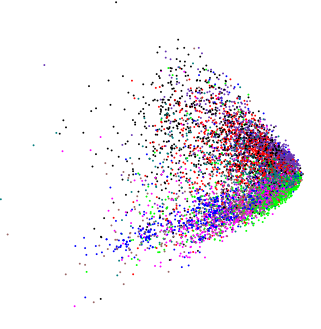 .
.
Durch Anwenden von PCA auf absolut unterschiedliche, leicht hochdimensionale Daten erhielt ich ein ähnlich aussehendes Diagramm:  (außer in diesem Fall wollte ich wirklich wissen, ob es eine interne Struktur gibt).
(außer in diesem Fall wollte ich wirklich wissen, ob es eine interne Struktur gibt).
Wenn wir zufällige Daten in PCA einspeisen, erhalten wir einen scheibenförmigen Blob, sodass diese keilförmige Form nicht zufällig ist. Bedeutet es etwas für sich?
data-visualization
pca
Macleginn
quelle
quelle

Antworten:
Angenommen, die Variablen sind positiv oder nicht negativ, dann sind die Kanten der Kante nur Punkte, ab denen die Daten 0 bzw. negativ werden würden. Da solche realen Daten dazu neigen, recht schief zu sein, sehen wir eine größere Punktdichte am unteren Ende ihrer Verteilung und damit eine größere Dichte am "Punkt" des Keils.
Im Allgemeinen ist PCA einfach eine Rotation der Daten, und Einschränkungen für diese Daten werden in den Hauptkomponenten im Allgemeinen auf die gleiche Weise wie in der Frage gezeigt sichtbar.
Hier ist ein Beispiel mit mehreren logarithmisch normalverteilten Variablen:
Abhängig von der Rotation, die von den ersten beiden PCs impliziert wird, sehen Sie möglicherweise den Keil oder eine etwas andere Version, die hier in 3D mit (
ordirgl()anstelle vonplot()) angezeigt wird.Hier in 3d sehen wir mehrere Spitzen, die aus der Mittelmasse herausragen.
Und für einheitliche positive Zufallsvariablen sehen wir einen Würfel
Beachten Sie, dass ich hier zur Veranschaulichung die Uniform mit nur 3 Zufallsvariablen zeige, daher beschreiben die Punkte einen Würfel in 3d. Mit höheren Dimensionen / mehr Variablen können wir den 5d-Hyperwürfel nicht perfekt in 3D darstellen und daher wird die ausgeprägte "Würfel" -Form etwas verzerrt. Ähnliche Probleme betreffen die anderen gezeigten Beispiele, aber die Einschränkungen in diesen Beispielen sind immer noch leicht zu erkennen.
Für Ihre Daten würde eine Protokolltransformation der Variablen vor der PCA die Schwänze ziehen und die verklumpten Daten ausdehnen, genau wie Sie eine solche Transformation in einer linearen Regression verwenden könnten.
Andere Formen können in PCA-Plots auftreten. Eine solche Form ist ein Artefakt der in der PCA erhaltenen metrischen Darstellung und wird als Hufeisen bezeichnet . Für Daten mit einem langen oder dominanten Gradienten (Stichproben, die entlang einer einzelnen Dimension angeordnet sind, wobei Variablen entlang von Teilen der Daten von 0 auf ein Maximum ansteigen und dann wieder auf 0 abnehmen, sind dafür bekannt, solche Artefakte zu erzeugen
Dies erzeugt ein extremes Hufeisen, bei dem sich die Punkte an den Enden der Achsen in die Mitte zurückbiegen.
quelle