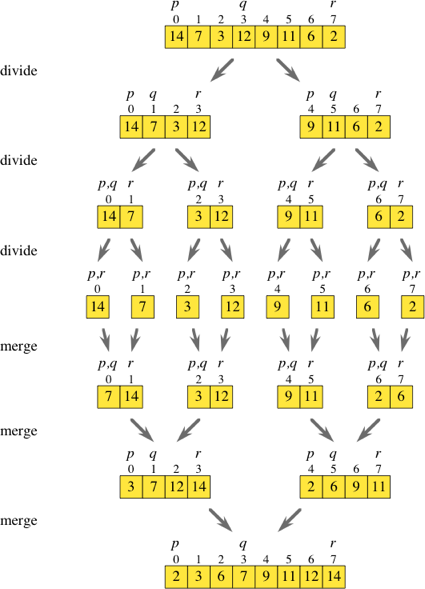
Merge Sort ist also ein Divide-and-Conquer-Algorithmus. Während ich mir das obige Diagramm ansah, überlegte ich, ob es möglich wäre, im Grunde alle Teilungsschritte zu umgehen.
Wenn Sie beim Springen um zwei über das ursprüngliche Array iterieren, können Sie die Elemente am Index i und i + 1 abrufen und sie in ihre eigenen sortierten Arrays einfügen. Sobald Sie alle diese Sub-Arrays ([7,14], [3,12], [9,11] und [2,6], wie im Diagramm gezeigt) haben, können Sie einfach mit der normalen Zusammenführungsroutine fortfahren ein sortiertes Array.
Ist es weniger effizient, durch das Array zu iterieren und die erforderlichen Unterarrays sofort zu generieren, als die Divisionsschritte in ihrer Gesamtheit auszuführen?
algorithms
sorting
efficiency
mergesort
Jimmy_Rustle
quelle
quelle

Antworten:
Die Verwirrung ergibt sich aus dem Unterschied zwischen der konzeptuellen Beschreibung des Algorithmus und seiner Implementierung .
Die logische Sortierung beim Zusammenführen wird als Aufteilen des Arrays in kleinere Arrays und anschließendes Zusammenführen dieser Arrays beschrieben. "Aufteilen des Arrays" bedeutet jedoch nicht "Erstellen eines völlig neuen Arrays im Speicher" oder ähnliches - es könnte in Code wie folgt implementiert werden
dh es findet keine eigentliche Arbeit statt, und die "Aufteilung" ist rein konzeptionell. Also, was Sie vorschlagen, funktioniert auf jeden Fall, aber logischerweise "spalten" Sie die Arrays immer noch auf - Sie brauchen nur keine Arbeit vom Computer, um dies zu tun :-)
quelle
1<<n+1. Ich bin mir jedoch sicher, dass Sie die Einstellungen so anpassen können, dass ein zu kleiner Schwanz in einem niedrigeren Durchgang zusammengeführt wird.Ich denke, was Sie meinen, ist die Bottom-up-Implementierung . In der Bottom-Up-Implementierung beginnen Sie mit einzelnen Zellenelementen und bewegen sich nach oben, indem Sie Elemente in größeren sortierten Listen / Arrays zusammenführen. Kehren Sie einfach die Pfeile in der obigen Abbildung um und beginnen Sie beim mittleren Array, dh bei Arrays mit einem Element.
Möglicherweise möchten Sie auch die Zusammenführungssortierung optimieren, indem Sie die Arrays teilen, bis sie eine konstante Größe erreichen. Anschließend sortieren Sie sie einfach mit der Einfügesortierung.
Andernfalls ist das Sortieren ohne Aufteilung des Arrays nicht möglich. Tatsächlich besteht der Kern der Sortierung "Zusammenführen" darin, Unterfelder zu unterteilen und zu sortieren, dh zu teilen und zu erobern.
quelle