Was wären die schlimmen Folgen von NP = PSPACE? Ich bin überrascht, dass ich dazu nichts gefunden habe, da diese Klassen zu den berühmtesten gehören.
Hätte dies insbesondere Konsequenzen für die unteren Schichten?
Was wären die schlimmen Folgen von NP = PSPACE? Ich bin überrascht, dass ich dazu nichts gefunden habe, da diese Klassen zu den berühmtesten gehören.
Hätte dies insbesondere Konsequenzen für die unteren Schichten?
Antworten:
Wenn , würde dies bedeuten:NP PSPACE
PSPACE
N PP#P NP
NP NP
Das heißt, das Zählen der Lösungen für ein Problem in wäre vielfach reduzierbar, um eine einzige Lösung zu finden.
Das heißt, polynomzeit-randomisierte Algorithmen mit einer Erfolgswahrscheinlichkeit von beliebig nahe 1/2 sind polynomzeitreduzierbar auf polynomzeit-randomisierte Algorithmen mit einseitigem Fehler, bei denen JA-Instanzen akzeptiert werden mit beliebig geringer Wahrscheinlichkeit;
Das heißt, für jedes Problem, das in der Polynomzeit überprüfbar ist, liefert die Randomisierung bestenfalls eine Beschleunigung der Polynomzeit (dies ist jedoch nur eine Folge der Kollapsierung der Polynomzeithierarchie).
Das heißt, jedes Problem, das von einem Quantencomputer gelöst werden kann, hat leicht Zertifikate für seine Antworten verifiziert. Dies wäre ein wichtiges positives Ergebnis in der Philosophie der Quantenmechanik und wahrscheinlich hilfreich für die Bemühungen, Quantencomputer zu konstruieren (um zu überprüfen, ob sie das tun, was sie tun sollen).
All dies liegt an den Containments der Klassen auf der linken Seite in (obwohl wir auch ).B Q P ⊆ P PPSPACE BQP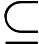 PP
PP
quelle
Ein Punkt, der implizit, aber noch nicht explizit erwähnt wurde, ist, dass wir . Obwohl dies gleichbedeutend ist mit zu , folgt dies direkt aus der Tatsache, dass unter complement geschlossen ist, was trivial zu beweisen ist.P H N P P S P A C ENP coNP
coNP PH NP PSPACE
Ich denke, ist es wert, allein darauf hinzuweisen, da es eine große Anzahl überraschender Konsequenzen gibt: Es gibt kurze Beweise, wenn ein Graph nicht dreifarbig ist, * nicht-* Hamiltonianer Wenn zwei Graphen * nicht * isomorph sind, ... und (in gewissem Sinne allgemeiner) gibt es ein Cook-Reckhow-Beweissystem, in dem jede Satz-Tautologie einen polynomgroßen Beweis hat.NP coNP
coNP
quelle
If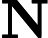







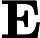
1) Die Polynom-Hierarchie würde zu .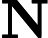

2) Wir werden jetzt da wir wissen, dassP S P A C E ≠ N L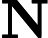


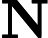
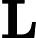





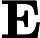

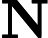
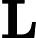
---AKTUALISIEREN---
3) Es ist bekannt, dass , wobei es sich um die logarithmisch raumbegrenzten Versionen von , bzw. . Dann könnte per Definition keine dieser Komplexitätsklassen gleich unter der Annahme, dass .N P C = P P P N P N P = P S P A C E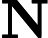
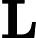



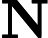






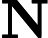

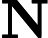







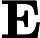
quelle
Zusätzlich zu den Ergebnissen in allen anderen Antworten darauf gibt es ein ein Interactive Proof - Systeme beteiligt ( ), dass die Verallgemeinerung ist wo Verifier und Prover tauschen Nachrichten aus, um die Sprache zu erkennen.N P


Es ist bekannt, dass , wenn also , bedeutet dies, dass nur eine Nachricht ausreicht! Für mich ist das beeindruckendere an diesem Ergebnis, dass der Prüfer den Prüfer nicht herausfordern müsste und der allerersten von ihr gesendeten Nachricht vertrauen kann.N P = P S P A C E














quelle