Warum unterrichten US- und UK-Schulen unterschiedliche Methoden zur Berechnung der Standardabweichung?

15

Soweit ich weiß, lehren die britischen Schulen, dass die Standardabweichung wie folgt ermittelt wird:

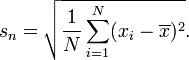
$Alt-Text$

in der Erwägung, dass US-Schulen unterrichten:

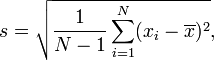
$Alt-Text$

(auf einer grundlegenden Ebene sowieso).

Dies hat in der Vergangenheit eine Reihe von Problemen meiner Schüler verursacht, da sie im Internet gesucht haben, aber die falsche Erklärung gefunden haben.

Warum der Unterschied?

Welcher Fehlergrad tritt bei einfachen Datensätzen mit 10 Werten auf, wenn die falsche Methode angewendet wird (z. B. bei einer Prüfung)?

standard-deviation error teaching unbiased-estimator Amos
quelle

4

Ich bin mir nicht sicher, ob es der Weg ist, das eine oder das andere als die „falsche“ Formel zu bezeichnen, um das Problem zu verstehen. Es ist nur so, dass die zweite in dem Sinne "besser" ist, dass sie ein unvoreingenommener Schätzer der wahren Standardabweichung ist. Wenn Sie sich also für unvoreingenommene Schätzungen interessieren, ist die zweite "besser" / "richtig".

Ich habe die Formel lediglich in dem Sinne als "falsch" charakterisiert, dass Sie bei einer Prüfung, wenn Sie die Formel verwenden, die nicht durch den Lehrplan vorgeschrieben ist, die Antwort "falsch" erhalten. Plus, wenn die Werte nicht eine Stichprobe der Bevölkerung an sich sind, dann gibt die erste Formel sicher den genaueren Wert.

Amos

13

Srikant, ich glaube nicht, dass der zweite ein unvoreingenommener Schätzer ist. Das Quadrat davon ist ein unvoreingenommener Schätzer der wahren Varianz. Jensens Ungleichung legt jedoch fest, dass die Erwartung einer krummlinigen Funktion einer Zufallsvariablen nicht mit der Erwartungsfunktion der Zufallsvariablen identisch ist. Daher kann die zweite Formel kein unvoreingenommener Schätzer der wahren Standardabweichung sein.

Andrew Robinson

Als Querverweis: Es wurde auch nach @ m.SE gefragt ...

JM ist kein Statistiker

2

Jede US - Schule , die sehr beliebt elementaren Text mit von Freedman, Pisani, & Purves ist mit der ersten Formel (

), so dass es falsch scheint dies als US vs. UK Unterschied zu charakterisieren.

s_{n}

$s_n$

Whuber

18

Die erste Formel ist die Populationsstandardabweichung und die zweite Formel ist die Stichprobenstandardabweichung . Die zweite Formel bezieht sich auch auf den unverzerrten Schätzer der Varianz - siehe Wikipedia für weitere Details.

Ich nehme an, (hier) in Großbritannien wird nicht zwischen Stichprobe und Grundgesamtheit an der High School unterschieden. Sie berühren sicherlich keine Konzepte wie voreingenommene Schätzer.

csgillespie
quelle

4

Colin, ein unverzerrter Schätzer der Standardabweichung, hat im allgemeinen Fall keine geschlossene Darstellung. Was existiert, ist der unvoreingenommene Schätzer der Varianz (s 2 in diesem Fall). Bemerkenswert ist, dass beide konsistente Schätzer der Populationsvarianz sind - und somit nach dem kontinuierlichen Kartierungssatz die beiden Schätzer der Standardabweichungen. Ein verwandter Punkt ist, dass s n 2 eine niedrigere MSE als s 2 hat. Der zusätzliche Vorteil der Unparteilichkeit ist fraglich.

Mornington

@Tirthankar - sehr schlampig von mir. Ich habe die Antwort leicht geändert. Vielen Dank.

csgillespie

2

Soweit ich mich erinnere, wurde mir die „Stichprobenberechnung“ in GCSE Mathematik und Naturwissenschaften (Alter 14-16) beigebracht, und die Unterscheidung zwischen Populationen und Stichproben und den damit verbundenen Varianzmaßen wurde auf A-Level behandelt (wenn auch nicht eingehend) ( Alter 16-18). Ich bin mir also nicht sicher, ob dies ein einfacher Unterschied zwischen Großbritannien und den USA ist.

Freya Harrison

11

Da noch niemand die letzte Frage beantwortet hat, nämlich die Unterschiede zwischen den beiden Formeln zu quantifizieren, sollten wir uns darum kümmern.

Aus vielen Gründen ist es angebracht, Standardabweichungen eher in Bezug auf ihre Verhältnisse als in Bezug auf ihre Unterschiede zu vergleichen. Das Verhältnis ist

s_{n} / s = \sqrt{\frac{N - 1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2 N} .

$s_n / s = \sqrt{\frac{N-1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2N}.$

$|\binom{1/2}{2}N^{-2}|$ $1 / (8 N^2)$ $N$ $2$

$N$ $5$ $N$ $10$ SDs, z. B. beim Vergleich der Spreads zweier Datensätze. (Wenn die Datensätze gleich zahlreich sind, verschwinden die Diskrepanzen praktisch vollständig und beide Formeln führen zu identischen Schlussfolgerungen.) Dies sind wohl die Argumentationsformen, die wir versuchen, Anfängern beizubringen. Wenn die Schüler sich also Gedanken darüber machen, welche Formel sie verwenden sollen, Dies könnte als Zeichen dafür gewertet werden, dass der Text oder die Klasse nicht das hervorhebt, was wirklich wichtig ist.

$N$ $t$ $z$ $s$ $s_n$

whuber
quelle

6

Dies ist Bessels Korrektur . Die US-Version zeigt die Formel für die Standardabweichung der Stichprobe , wobei die obige UK-Version die Standardabweichung der Stichprobe ist .

Reed Copsey
quelle

5

Ich bin mir nicht sicher, ob dies eine reine US-amerikanische oder eine britische Angelegenheit ist. Hier ist eine kurze Seite, die ich geschrieben habe , um den Unterschied zwischen der Verwendung von n und n-1 bei der Berechnung einer Standardabweichung zu erläutern .

Harvey Motulsky
quelle

1

Ich habe es nicht so gemeint, ich war nur neugierig, warum ein solcher Unterschied entstanden sein könnte, welche Art von Fehler durch falsche Ratschläge entstehen könnte und ob es eine anständige Erklärung für den Unterschied gibt, den ich meinen Schülern geben könnte .

Amos

3

Da N die Anzahl der Punkte im Datensatz ist, könnte man argumentieren, dass man durch die Berechnung des Mittelwerts den Freiheitsgrad im Datensatz um eins verringert hat (da man eine Abhängigkeit in den Datensatz eingeführt hat), also sollte man N verwenden -1 bei der Schätzung der Standardabweichung von einem Datensatz, für den zuvor der Mittelwert geschätzt werden musste.

Benjamin Bannier
quelle

Warum unterrichten US- und UK-Schulen unterschiedliche Methoden zur Berechnung der Standardabweichung?

Antworten: